Regresja liniowa jest najprostszym wariantem regresji (przeczytaj najpierw o idei regresji) w statystyce. Zakłada ona, że zależność pomiędzy zmienną objaśnianą a objaśniająca jest zależnością liniową. Tak jak w analizie korelacji, jeżeli jedna wartość wzrasta to druga wzrasta (dodatnia korelacji) lub spada (korelacja ujemna). W regresji liniowej zakłada się, że wzrostowi jednej zmiennej (predyktor, predyktory) towarzyszy wzrost lub spadek na drugiej zmiennej. Co więcej, nazwa regresji liniowej odnosi się, że funkcja regresji przyjmuje postać funkcji liniowej, czyli y = bx+a.
Analiza regresji liniowej ma na celu wyliczenie takich współczynników regresji (współczynników w modelu liniowym), aby model jak najlepiej przewidywał wartość zmiennej zależnej, aby błąd oszacowania był jak najmniejszy. Tak więc analiza regresji "dopasowuje" taką linię prostą do badanych (liniowa zależność), aby jak model był jak najlepszy (obarczony jak najmniejszym błędem losowym). Przyjrzyjmy się poniższemu przykładowi:
Badacz badał związek pomiędzy poziomem inteligencji uczniów a ich ocenami uzyskiwanymi na koniec roku z matematyki. Na wykresie rozrzutu poniżej przedstawiono uzyskane wyniki.
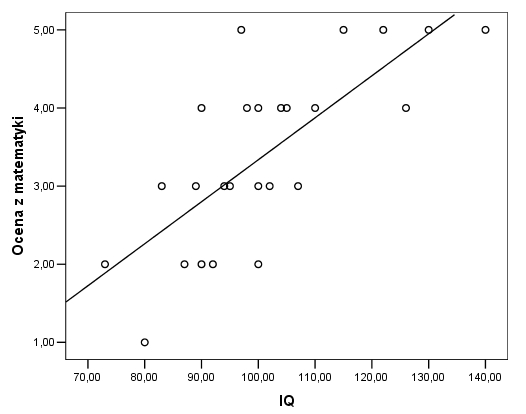
Jak można zauważyć, zależność pomiędzy IQ a ocenami z matematyki jest liniowa, im wyższy poziom IQ tym lepsze oceny z matematyki. Oczywiście zależność ta nie jest idealna, nie zawsze osoby, które mają niższy IQ mają gorsze oceny od osób, które mają wyższe IQ, co widać na wykresie.
Aby wyznaczyć linię regresji, a tym samym wzór modelu regresji liniowej należy obliczyć współczynniki linii prostej, a i b. W tym celu wykorzystuje się metodę najmniejszych kwadratów błędu. Nie wchodząc tutaj w szczegóły obliczeniowe metoda ta dostarcza nam takich współczynników a i b, które powodują, że linia regresji jest najlepiej dopasowana do zebranych danych. Wracając do wzory na linię prostą, analiza regresji oblicza współczynnik b, zwany współczynnikiem regresji oraz wartość a, zwany wyrazem wolnym.
Gdy poprzez analizę regresji liniowej oszacujemy wzór regresji, wzór na linię prostą w modelu, czyli nasze współczynniki a i b, to będziemy mogli oszacować wartości zmiennej zależnej (zmiennej objaśnianej, Y) na podstawie wartości predyktora (zmienna objaśniająca, X) podstawiając odpowiednią wartość X do uzyskanego wzoru. Dlatego też mówimy, że analiza regresji służy do przewidywania wartości jednej zmiennej na podstawie innych.
Oczywiście opisany wyżej przykład dotyczył prostej analizy regresji liniowej, z uwzględnieniem tylko jednego predyktora. W tym przypadku modeli regresji wielorakiej, wielokrotnej, gdy mamy większą liczbę predyktorów stosujemy następujący wzór na linię regresji:
\(Y = b_1X_1 + b_2X_2 + ... + b_nX_n + a\), gdzie:
Y = b1X1 + b2X2+...+bnXn + a, gdzie:
\(b_1, b_2, b_n\) są współczynnikami regresji wyliczonymi dla poszczególnych predyktorów w modelu
\(X_1, X_2, X_n\) są wartościami predyktorów
\(Y\) to zmienna objaśniana, zmienna zależna
\(a\) to wyraz wolny
Graficzną interpretacją linii regresji dla dwóch predyktorów nie będzie już linia prosta lecz płaszczyzna w układzie trójwymiarowym.
Analiza regresji dostarcza nam informacji, czy poszczególne predyktory wprowadzone do modelu liniowego są istotne statystycznie, tzn, czy któryś z nich jest "zbędny" dla oszacowania zmiennej zależnej. Analiza regresji dostarcza nam wielkości błędu oszacowania wartości wyników (z założonym prawdopodobieństwem) oraz dostarcza nam na ile model regresji liniowej wyjaśnia zaobserwowaną wariancję wyników zmiennej zależnej (współczynnik R-kwadrat, determinacji). Jeżeli model okazuje się być istotny statystycznie to okazuje się on "przydatny" do oszacowania wartości zmiennej zależnej na podstawie wartości predyktora, predyktorów.
W analizie regresji liniowej zmienne wprowadzane do modelu: zmienna zależna i predyktory muszą mieć postać ilościową, nie mogą być to zmienne nominalne czy porządkowe. Oczywiście istnieją rodzaje analiz regresji, gdzie takie zmienne można modelować, jednakże nie jest to już regresja liniowa.
Analiza regresji liniowej jest najczęściej spotykanym rodzajem analizy regresji w ogóle. Powodem tego jest względna prostota tego sposobu analizy danych. Interpretacja funkcji regresji dotyczy przydatności poszczególnych predyktorów w modelu regresji do przewidywania poziomu zmiennej zależnej.
Regresja liniowa Wasze opinie
Podobnie jak rosół, warto wcześniej "pyrkać" ją nawet przez kilka godzin, aby smaki odpowiednio się przegryzły. Nie ma lepszego przepisu na idealną zupę, niż cierpliwość.