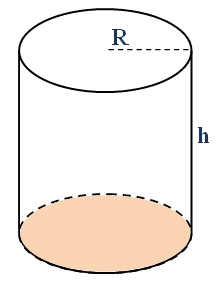
Wzór na pole powierzchni walca obrotowego ma postać:\(P = 2 P_p + P_b\)
\(P_p = \pi R^2\)
\(P_b = 2 \pi R h\)
\(P = 2 \pi R^2 + 2 \pi R h = 2 \pi R (R + h)\)
Wyjaśnienie symboli:
\(P\) - pole powierzchni całkowitej walca obrotowego
\(P_p\) - pole podstawy walca obrotowego
\(P_b\) - pole powierzchni bocznej walca obrotowego
\(P\) - pole powierzchni całkowitej walca obrotowego
\(R\) - promień podstawy walca obrotowego (koła)
\(h\) - wysokość walca obrotowego
Wzór na pole powierzchni walca obrotowego - jak stosować w praktyce?