Kwartet Anscombe'a powstał w 1973 roku za sprawą Francisa Anscombe'a. Jest to zestaw czterech układów danych, które mają takie same cechy statystyczne (mamy tu na myśli średnią arytmetyczną, wariancję, współczynnik korelacji oraz równanie regresji liniowej), ale jednocześnie wyglądają różnie przy przedstawieniu graficznym.
Nie jest do końca jasne, skąd sam Anscombe wziął swoje dane. Poniżej znajdują się dane wyjściowe, których użył do przedstawienia omawianej problematyki:
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
Mamy tutaj cztery zestawy danych, w każdym jest po 11 obserwacji.
W każdym przypadku mamy dokładnie takie same wyniki obliczeń.
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | |
| średnia | 9 | 7.50 | 9 | 7.50 | 9 | 7.50 | 9 | 7.50 |
| wariancja | 11 | 4.12 | 11 | 4.12 | 11 | 4.12 | 11 | 4.12 |
Współczynnik korelacji między zmiennymi y oraz x: 0.816, natomiast wzór regresji liniowej: \(y=3+0.5x\)
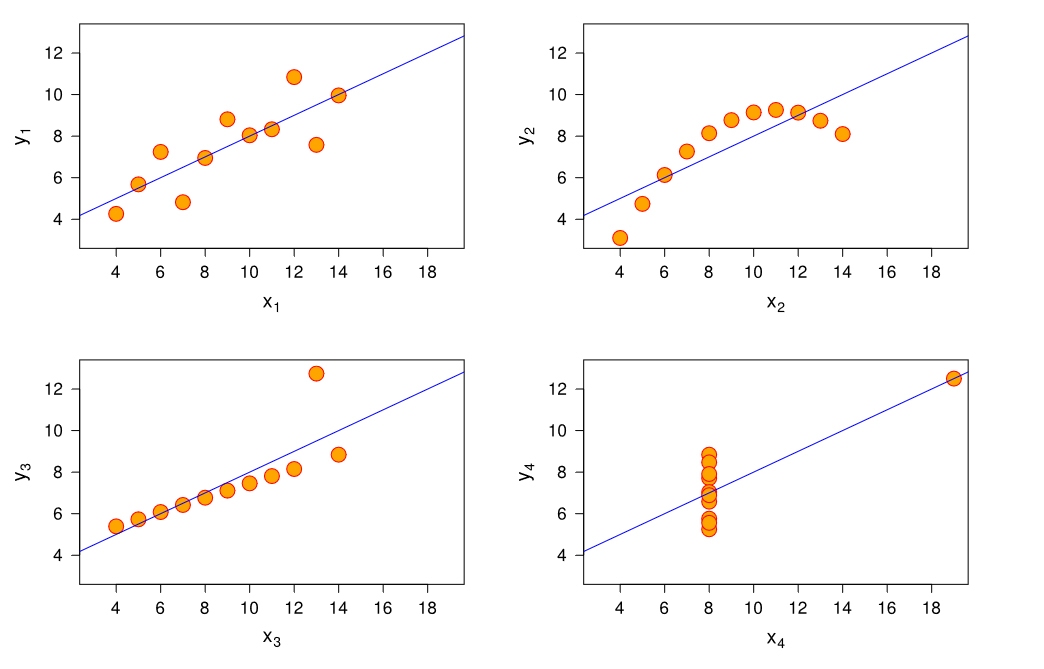
Wydawać by się mogło, że wszystkie zestawy danych muszą być podobne. W końcu cechy statystyczne są identyczne, ale wystarczy spojrzeć na wykresy, które pokazują, że nie wszystko jest takie same.
Powyższe przedstawienie graficzne zestawów danych ilustruje różnice pomiędzy nimi. Mamy tu do czynienia z wykresami punktowymi. Pierwszy wykres wydaje się być liniowy; odpowiada on dwóm zmiennym skorelowanym. Drugi wykres nie jest rozłożony normalnie; związek pomiędzy dwoma zmiennymi wydaje się być oczywisty, ale sam wykres nie jest liniowy. Trzeci wykres przedstawia rozkład liniowy, jednakże obliczona regresja kompensowana jest przez jedną wartość odstającą, która ma dość mocny wpływ na współczynnik korelacji. Jeżeli zaś chodzi o czwarty wykres, jest to dobry przykład na to, jak jedna obserwacja wysokiej dźwigni wystarczy do wytworzenia wysokiego współczynnika korelacji, nawet jeśli inne punkty nie będą wskazywać na bezpośredni związek pomiędzy zmiennymi.
Sam Anscombe skupił się jedynie na miarach klasycznych, nie patrząc na miary pozycyjne. Jego celem było pokazanie, że nie tylko obliczenia są ważne, ale także rysunki, wykresy. Jest to dobry przykład wartości wizualizacji danych - wykres czasem potrafi nam więcej opowiedzieć niż zaawansowany model statystyczny.
Kwartet Anscombe'a Wasze opinie