Na wykresach poniżej przedstawiamy przykłady zmiennych o ujemnej i dodatniej wartości kurtozy.
Kurtoza ujemna, rozkład platokurtyczny
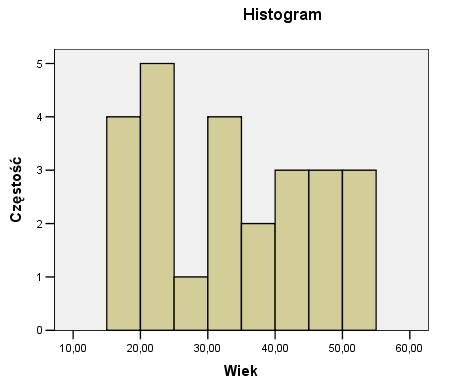
Przykładem zmiennej o ujemnej kurtozie może być wiek uczestników pewnego turnieju szachowego. Jak wiadomo, grą w szachy interesują się osoby w różnym wieku. Do turnieju zgłosiła się podobna liczba osób w młodym, średnim i starszym wieku. Średnia wieku wyniosła około 33 lat (30-35 lat), jednakże jak zobaczymy na powyższym histogramie osób w tym wieku jest podobna liczba co osób w innych grupach wiekowych.
Kurtoza dodatnia, rozkład leptokurtyczny
Kurtoza ujemna, rozkład platokurtyczny

Przykładem zmiennej o ujemnej kurtozie może być wiek uczestników pewnego turnieju szachowego. Jak wiadomo, grą w szachy interesują się osoby w różnym wieku. Do turnieju zgłosiła się podobna liczba osób w młodym, średnim i starszym wieku. Średnia wieku wyniosła około 33 lat (30-35 lat), jednakże jak zobaczymy na powyższym histogramie osób w tym wieku jest podobna liczba co osób w innych grupach wiekowych.

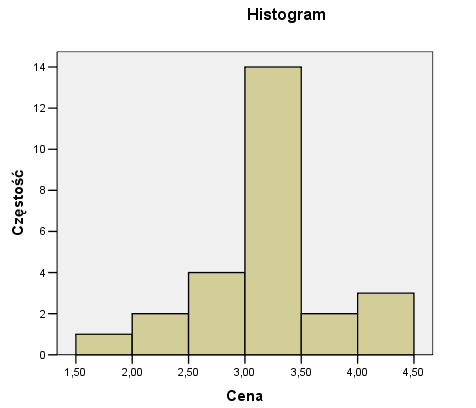
Przykładem zmiennej o dodatniej kurtozie może być cena kilograma jabłek (dane hipotetyczne) w sierpniu w danym mieście w Polsce. Badacz zbadał cenę w kilkunastu miejscach, w których sprzedawane są jabłka. Średnia cena wyniosła około 3zł. Jak widać na histogramie powyżej, w zdecydowanej większości sklepów / targów cena za kilogram jabłek wynosi około 3zł, jest niewiele sklepów, gdzie cena ta jest wyższa bądź niższa od średniej ceny z przeprowadzonego badania.
Wykresy rozkładów o różnej kurtozie Wasze opinie