Przykład rozkładu Gaussa
Poziom inteligencji. Najwięcej jest osób o średnim poziomie inteligencji, IQ = 100. O wiele mniej osób ma poziom inteligencji równy IQ = 80, czy IQ = 120, a jeszcze mniej, IQ = 65, czy IQ = 135.
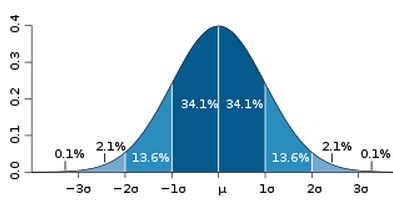
Jak można zauważyć, około 68% obserwacji znajduje się blisko średniej, w odległości jednego odchylenia standardowego od średniej (miary odległości w języku statystyki). Wraz z odsuwaniem się od średniej krzywa Gaussa opada. W odległości dwóch odchyleń standardowych znajduje się aż 95% obserwacji. Wartości skrajne (na krańcach krzywej Gaussa) reprezentowane są przez znikomy procent obserwacji.
Wzór na funkcję gęstości rozkładu normalnego
Wzór na funkcję gęstości rozkładu normalnego
Jedynymi niewiadomymi są tu właśnie średnia i odchylenie standardowe. Po co nam określenie rozkładu normalnego? Po to, aby dla zaobserwowanych zmiennych (inny będzie średni wynik IQ = 100; inny będzie średni wynik wieku, np. 45 lat) wiedzieć, na ile zaobserwowane wyniki u poszczególnych obserwacji, osób odchylają się od wartości średniej.
Zastosowanie rozkładu normalnego
Wracając do praktyki: Rozkład normalny można nazwać najbardziej "pożądanym" rozkładem. Powodem tego jest fakt, że rozkład normalny dokładnie opisuje losowe przypadki. Gdy obserwujemy jakieś losowe czynniki w naturze, np. średni poziom inteligencji u losowo wybranych 20 osób, to raz możemy uzyskać wynik, np. 110, drugim razem 98, ale gdy powtórzylibyśmy takie badanie wielokrotnie to pomimo, iż losowo wybieraliśmy osoby do badania, średnia dla takich pomiarów wyniosłaby 100 (zakładając, że faktycznie średni poziom IQ w całej populacji wynosi 100). Do tego, pomiary skrajne będą występowały o wiele rzadziej niż pomiary o przeciętnym wyniku.
To sprawia, że gdy rozkłady mierzonych przez nas zmiennych są zbliżone do rozkładu normalnego to możemy powiedzieć, że nie występują w naszej próbie "anomalia", nasze dane są "normalne", występuje niewiele obserwacji skrajnych a znaczna cześć obserwacji jest skoncentrowana wokół średniej. Dlatego też ważne jest, aby rozkłady były zbliżone do normalnego, aby nie obliczać wyników na "nienormalnej", niestandardowej próbie wyników, z np. nadreprezentacją wyników skrajnych. Występowanie takich anormalnych rozkładów sprawia, że nie można dla nich zastosować właściwości rozkładu normalnego, a co za tym idzie, nie można skorzystać z wielu statystycznych testów, ponieważ ich rezultaty mogą być zaburzone poprzez występowanie niestandardowego rozkładu wyników.
W celu oszacowania czy rozkład empirycznej zmiennej (badanej, mierzonej) jest zbliżony do rozkładu normalnego przeprowadza się testy np. test Shapiro-Wilka lub test Kołmogorowa-Smirnowa.
Rozkład normalny. Rozkład Gaussa Wasze opinie