Czy ciag \(a_n=n^2-n-12\) posiada wyrazy ujemne, jeśli tak to jakie?
Aby uzyskać odpowiedź, trzeba rozwiązać nierówność \(a_n<0\).
\(a_n<0\)
\( n^2-n-12<0\)
Następnie trzeba rozwiązać nierówność kwadratową.
\( \Delta=(-1)^2-4\cdot 1\cdot (-12)=1+48=49\)
\(\sqrt{\Delta}=\sqrt{49}=7\)
\(n_1=\dfrac{1-7}{2\cdot 1}\:\:\:\:\:\:\:\:\:\:\: n_2=\dfrac{1+7}{2\cdot 1}\)
\(n_1=-3 \:\:\:\:\:\:\:\:\:\: n_2=4\)
Dla lepszego zobrazowania i zinterpretowania wyników, najlepiej narysować odręczny wykres, który jest parabolą z ramionami skierowanymi ku górze ponieważ \(n^2\) jest z współczynnikiem dodatnim.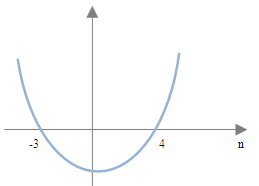
Szukane są liczby naturalne, które znajdują się w przedziale (-3;4) ponieważ wartości ciągu mają być mniejsze od zera, czyli pod osią \(n\). Szukane wyrazy to \(1;2;3\).
Odpowiedź: Podany ciąg \(a_n\) posiada trzy wyrazy ujemne, są nimi \(a_1; a_2; a_3\).
Zadanie 1
Zadanie 2
Zadanie 3
Zadanie 4
Zadanie 6
Aby uzyskać odpowiedź, trzeba rozwiązać nierówność \(a_n<0\).
\(a_n<0\)
\( n^2-n-12<0\)
Następnie trzeba rozwiązać nierówność kwadratową.
\( \Delta=(-1)^2-4\cdot 1\cdot (-12)=1+48=49\)
\(\sqrt{\Delta}=\sqrt{49}=7\)
\(n_1=\dfrac{1-7}{2\cdot 1}\:\:\:\:\:\:\:\:\:\:\: n_2=\dfrac{1+7}{2\cdot 1}\)
\(n_1=-3 \:\:\:\:\:\:\:\:\:\: n_2=4\)
Dla lepszego zobrazowania i zinterpretowania wyników, najlepiej narysować odręczny wykres, który jest parabolą z ramionami skierowanymi ku górze ponieważ \(n^2\) jest z współczynnikiem dodatnim.

Szukane są liczby naturalne, które znajdują się w przedziale (-3;4) ponieważ wartości ciągu mają być mniejsze od zera, czyli pod osią \(n\). Szukane wyrazy to \(1;2;3\).
Odpowiedź: Podany ciąg \(a_n\) posiada trzy wyrazy ujemne, są nimi \(a_1; a_2; a_3\).
Zadanie 1
Zadanie 2
Zadanie 3
Zadanie 4
Zadanie 6
Jak obliczyć wzór ogólny ciągu - zadanie 5 - wyniki