Wskaż wszystkie wyrazy ciągu \(a_n=-n^2+10n-6\), których wartość jest większa od 3.
Aby rozwiązać zadanie trzeba rozwiązać równanie \( a_n\leqslant 3\), pamiętając, że \(n\) są liczbami naturalnymi.
\(a_n> 0\\
\(-n^2+10n-6 >3\)
\(-n^2+10n-6 -3>0\)
\(-n^2+10n-9>0\)
Następnie rozwiązujemy nierówność kwadratową.
\(\Delta = 10^2-4\cdot (-1)\cdot (-9)=100-36=64\)
\(\sqrt{\Delta}=\sqrt{64}=8\)
\(n_1=\dfrac{-10-8}{2\cdot (-1)}\:\:\:\:\:\:\:\:\:\:n_2=\dfrac{-10+8}{2\cdot (-1)}\)
\(n_1=9 \:\:\:\:\:\:\:\:\:\:\:n_2=1\)
Aby w łatwy sposób zinterpretować rozwiązanie najlepiej narysować wykres, wiedząc, że przy \(n^2\) mamy współczynnik dodatni, co oznacza, że ramiona paraboli są skierowane w dół.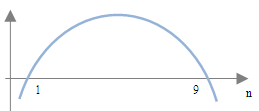
Szukane wyniki mają być większe od zera czyli znajdować się nad osią poziomą \(n\), muszą również być liczbami naturalnymi. Wszystkie liczby spełniające ten warunek to: 2,3,4,5,6,7,8. Oznacza to, że szukane wyrazy ciągu to: \(a_2; a_3; a_4; a_5; a_6; a_7; a_8\).
Odpowiedź: Szukanymi wyrazami ciągu \(a_n\), są wyrazy: \(a_2; a_3; a_4; a_5; a_6; a_7; a_8\).
Zadanie 1
Zadanie 2
Zadanie 3
Zadanie 4
Zadanie 5
Aby rozwiązać zadanie trzeba rozwiązać równanie \( a_n\leqslant 3\), pamiętając, że \(n\) są liczbami naturalnymi.
\(a_n> 0\\
\(-n^2+10n-6 >3\)
\(-n^2+10n-6 -3>0\)
\(-n^2+10n-9>0\)
Następnie rozwiązujemy nierówność kwadratową.
\(\Delta = 10^2-4\cdot (-1)\cdot (-9)=100-36=64\)
\(\sqrt{\Delta}=\sqrt{64}=8\)
\(n_1=\dfrac{-10-8}{2\cdot (-1)}\:\:\:\:\:\:\:\:\:\:n_2=\dfrac{-10+8}{2\cdot (-1)}\)
\(n_1=9 \:\:\:\:\:\:\:\:\:\:\:n_2=1\)
Aby w łatwy sposób zinterpretować rozwiązanie najlepiej narysować wykres, wiedząc, że przy \(n^2\) mamy współczynnik dodatni, co oznacza, że ramiona paraboli są skierowane w dół.
Odpowiedź: Szukanymi wyrazami ciągu \(a_n\), są wyrazy: \(a_2; a_3; a_4; a_5; a_6; a_7; a_8\).
Zadanie 1
Zadanie 2
Zadanie 3
Zadanie 4
Zadanie 5
Jak obliczyć wzór ogólny ciągu - zadanie 6 - wyniki