Bryły obrotowe - opis

Bryłą obrotową nazywamy bryłę geometryczną, która jest ograniczona powierzchnią powstałą w wyniku obrotu figury płaskiej dookoła prostej zwanej osią obrotu. 

• WALEC - powstaje w wyniku obrotu dowolnego prostokąta wokół prostej zawierającej jeden z jego boków.

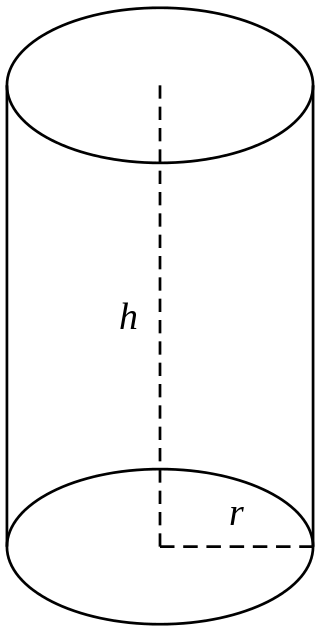
Podstawowe wzory:

\(P_p = {\pi r^2}\) pole powierzchni podstawy walca

\(P_b = {2\pi rh}\) pole powierzchni bocznej walca

\(P_c = 2P_p + P_b = {2\pi r^2 +2 \pi rh = 2\pi r (r+h)}\)pole powierzchni całkowitej walca

\(V = {\pi r^2 h}\) objętość walca

• STOŻEK - powstaje przez obrót trójkąta prostokątnego wokół jednej z przyprostokątnych. Przyprostokątna ta tworzy wysokość stożka, natomiast druga przyprostokątna jest promieniem podstawy, a przeciwprostokątna trójkąta prostokątnego staje się tworzącą stożka.

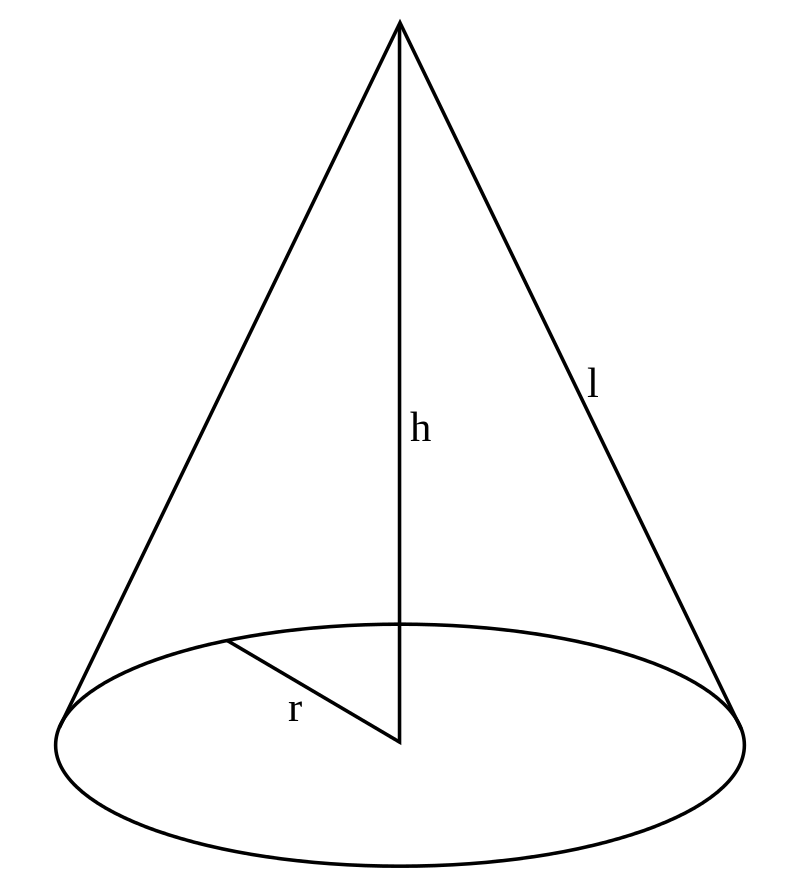
Podstawowe wzory (S - pole powierzchni stożka, h - wysokość stożka):

\(V= {{1\over 3}Sh}\) objętość stożka

\(P_p = {\pi rl}\)  pole powierzchni bocznej stożka

\(P_c = P_b +P_p = {\pi rl + \pi r^2 = \pi r (r+l)}\)pole powierzchni całkowitej stożka

\(tg {\alpha \over 2} = rh\) kąt rozwarcia stożka (kąt przy wierzchołku przekroju osiowego stożka)

\(l = {\sqrt{r^2+h^2}}\) długość tworzącej stożka (tworząca stożka to odcinek, który łączy dowolny punkt na brzegu podstawy stożka z jego wierzchołkiem lub najbliższym punktem na brzegu drugiej podstawy)

• KULA - powstaje przez obrót dowolnego koła wokół jego średnicy; powierzchnię kuli nazywamy sferą.

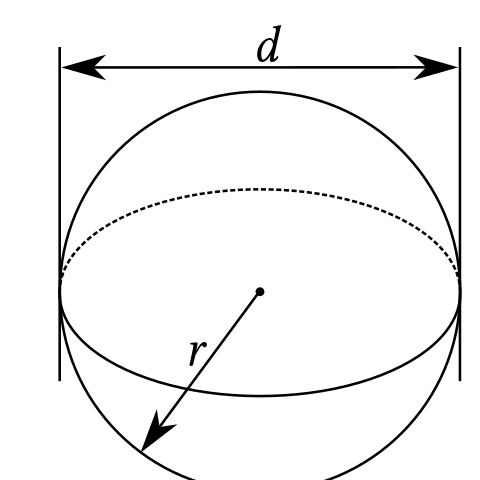
źródło: https://commons.wikimedia.org/wiki/File:Sphere_(parameters_r,d),_simple.svg

Podstawowe wzory:

\(P_p = {4 \pi r^2}\) pole powierzchni kuli (sfery)

\(V = {{4 \over 3 }{\pi r^3}}\)  objętość kuli