Fala dźwiękowa jest wytwarzana najczęściej przez drgającą powierzchnię (płytkę) która przekazuje drgania powietrzu. Fala dźwiękowa porusza się z prędkością \(v\) od źródła. Dla zobrazowania rysunek poniżej.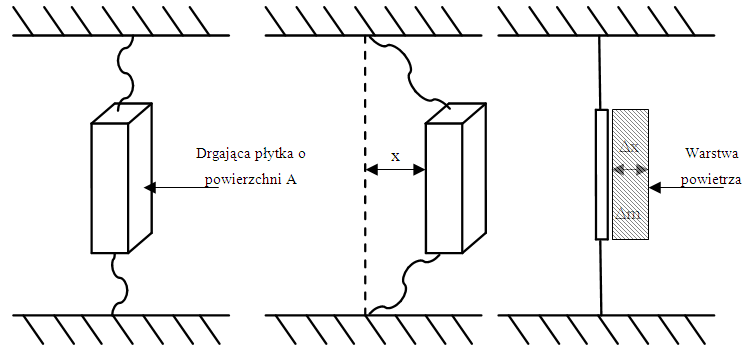



Do obliczenia energii fali dźwiękowej posłużmy się wzorem na energie kinetyczną:

\(\Delta E = \dfrac{1}{2}\Delta m\cdot v^2= \dfrac{1}{2}\Delta m\cdot \omega ^2\cdot x^2=

\dfrac{1}{2}(\varrho \cdot A \cdot \Delta x)\cdot \omega ^2\cdot x^2\)

w skrócie

\(\Delta E = \dfrac{1}{2}(\varrho \cdot A \cdot \Delta x)\cdot \omega ^2\cdot x^2\)

gdzie:

\(\Delta E\) - energie fali dźwiękowej [J],

\(\varrho\) – gęstość powietrza \( \left [ \dfrac{kg}{m^3} \right ]\),

\(x\) – amplituda drgań płytki harmonicznie drgającej [m],

\(\Delta x\) – odległość jaką przebywa zaburzenie [m],

\(\omega\) – pulsacja [rad/s], \(\omega=2\pi f\), gdzie f to częstotliwość drgań [Hz].

W ruchu harmonicznym prostym średnia energia potencjalna jest równa średniej energii kinetycznej. Idąc tym tokiem rozumowania, można uzyskać informację ile energii jest zawarte w warstwie powietrza o przekroju A i grubości Δx.
 
Dzieląc obie strony równania przez Δt możemy łatwo obliczyć moc P fali dźwiękowej.