Statystyka - opis

MEDIANA (inaczej przeciętna lub drugi kwartyl) – to wartość środkowa, która dzieli liczbę obserwacji na pół. Aby obliczyć medianę trzeba mieć zawsze uporządkowany zbiór wartości rosnący lub malejący.

• Mediana dla grupy danych o nieparzystej liczbie obserwacji: należy najpierw uporządkować dane, po czym znaleźć wartość pośrodku.

           Przykład 1. Wyznacz medianę z ciągu danych: 1, 2, 2, 7, 10, 14, 14, 22, 23.
           Powyższy ciąg składa się z ciągu 9 uporządkowanych liczb. dokładnie pośrodku znajduje się 10 (piąta liczba), mamy cztery
           wartości na prawo i na lewo od niej M=10

• Mediana dla grupy danych o parzystej liczbie obserwacji: należy najpierw uporządkować dane, i wyliczyć średnią arytmetyczną z dwóch wartości środkowych.

            Przykład 2. Wyznacz medianę z ciągu danych: 1, 2, 2, 7, 10, 14, 14, 22.
            Aby po lewej i prawej stronie znajdowała się taka sama ilość danych musimy wybrać dwie środkowe wartości czyli 7 i 10. \(M= {7+10 \over 2}=8,5\)

GRAFICZNE PRZEDSTAWIANIE MEDIANY - rysujemy linie n2 do momentu aż przetnie histogram, następnie rysujemy prostą łącząca dwa punkty w którym prostokąt z medianą styka się z sąsiednimi prostokątami:

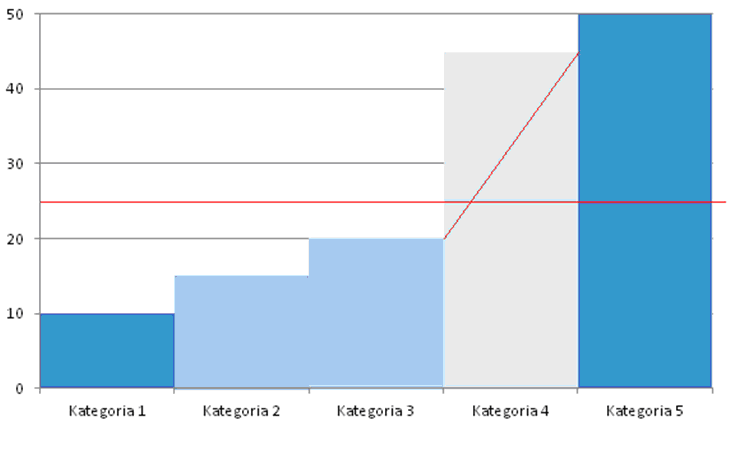
MODA (dominanta, wartość modalna) - Jest to wartość, która w danych statystycznych pojawia się najczęściej, aby wyznaczyć wartość modalną powinno się uporządkować rosnąco lub malejąco zbiór wartości. 

• Wyznaczanie wartości modalnej ze zbioru, którym jest tylko jedna dominanta

            Przykład 3. Wyznacz wartość modalną z ciągu danych: 1, 2, 2, 2, 7, 10, 14, 14, 22, 23.
            Wartością najczęściej występującą jest (dominującą) jest D=2.

• Wyznaczanie wartości modalnej ze zbioru, którym są dwie dominanty

            Przykład 4. Wyznacz wartość modalną z ciągu danych: 1, 2, 2, 7, 10, 14, 14, 22, 23.
            W tym przypadku mamy dwie najczęściej występujące wartości D₁=2 i D₂=14

• Wyznaczanie wartości modalnej ze zbioru, którym w którym wszystkie wartości występują z równą częstością

            Przykład 5. Wyznacz wartość modalną z ciągu danych: 1, 2, 7, 10, 14, 22, 23, 27, 29.
            W przypadku, gdy wszystkie wartości występują z taka samą częstością nie ma dominanty

GRAFICZNE PRZEDSTAWIANIE DOMINANTY - Wybieramy na histogramie najliczniejszy (czyli najczęściej występujący) przedział. Rysujemy dwie linie łączące górne krawędzie najliczniejszego przedziału z górnymi krawędziami sąsiednich prostokątów. Punkt przecięcia wyznacza dominantę.

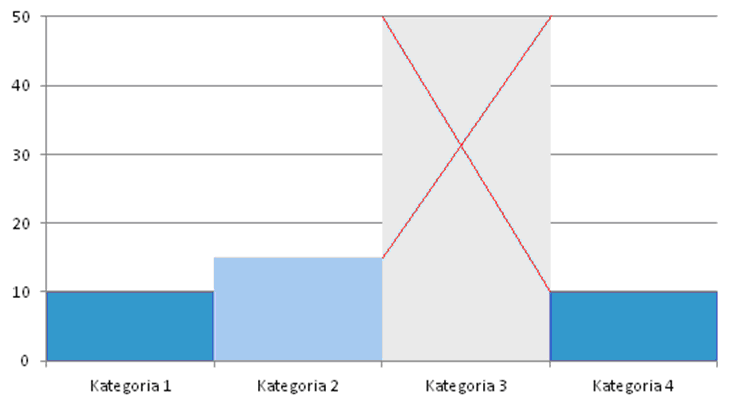
ŚREDNIA ARYTMETYCZNA – to suma wszystkich liczb podzielona przez ich ilość.

           Przykład 6. Oblicz średnią arytmetyczną liczb: 4, 2, 6, 4, 9
                                   x_śr=\({4+2+6+4+9 \over 5}=5\)