powrót do artykułu głównego Rozwiąż nierówności:
a) \(|x-5|+|x+6|>11\) b) \(|x+1|+|x-2|<4\)
c) \(|x+1|+|2-x|+|x-3|\leqslant 11\)
Aby rozwiązać nierówność tego typu najpierw podzielimy nierówność na kilka przypadków, zależnych od przyjmowanego znaku wyrażenia pod wartością bezwzględną.
Rozwiązanie
a)
\(|x-5|+|x+6|>11\)
Na początku postępujemy jak przy równaniu, czyli sprawdzamy, kiedy \(x-5\) oraz \(x+6\) przyjmuje wartości ujemne a kiedy większe bądź równe zero.
\(x-5 \geqslant 0 \:\:\:\:\:\:\: x+6 \geqslant 0\)
\(x \geqslant 5 \:\:\:\:\:\:\: x \geqslant -6\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania lepiej najpierw nanieść je na oś:

Rozwiązywanie nierówności podzielimy na trzy części zgodnie z przedziałami wyznaczonymi na osi.
1) dla \( x \: \epsilon \: (-\infty;-6)\)
Wyrażenia \(x-5\) oraz \(x+6\) w danym przedziale przyjmują wartości ujemne, dlatego przy opuszczaniu wartości bezwzględnych zmienimy ich znak.
\(|x-5|+|x+6|>11\)
\(-(x-5)-(x+6)>11\)
\(-x+5-x-6>11\)
\(-2x>11-5+6\)
\(-2x>12\)
\(x<-6\)
Rozwiązując nierówność otrzymaliśmy \(x \: \epsilon \: (-\infty,-6)\) należy to do przedziału więc \(x \: \epsilon \: (-\infty,-6)\) jest rozwiązaniem nierówności.
2) dla \( x \: \epsilon \: \left \langle -6;5 \right )\)
W podanym przedziale wyrażenie \(x-5\) przyjmuje wartości ujemne, dlatego opuszczając wartość bezwzględną zmienimy znak wyrażenia. Wyrażenie \(x+6\) w podanym przedziale przyjmuje wartości dodatnie, dlatego opuszczając wartość bezwzględna nie zmieniamy znaku wyrażenia.
\(|x-5|+|x+6|>11\)
\(-(x-5)+x+6>11\)
\(-x+5+x+6>11\)
\(11>11\)
Rozwiązując nierówność otrzymaliśmy wyrażenie sprzeczne, ponieważ 11 nie jest większe od 11. Oznacza to, że w przedziale \(\left \langle -6;5 \right )\) nie ma \(x\)-ów będących rozwiązaniem nierówności.
3) dla \( x \: \epsilon \: \left \langle 5;+\infty \right )\)
W podanym przedziale wyrażenia \(x-5\) oraz \(x+6\) przyjmując wartości dodatnie, oznacza to, że opuszczając wartość bezwzględną nie zmieniamy znaków wyrażeń.
\(|x-5|+|x+6|>11\)
\(x-5+x+6>11\)
\(2x>11+5-6\)
\(2x>10\)
\(x>5\)
Rozwiązując nierówność otrzymaliśmy \(x \epsilon (5;+\infty)\), należy on do naszego przedziału. Oznacza to, że rozwiązaniem nierówności jest \(x \epsilon (5;+\infty)\).
Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: (-\infty,-6) \: \cup \: (5;+\infty)\).
b)
\(|x+1|+|x-2|<4\)
Na początku sprawdzamy, kiedy \(x+1\) oraz \(x-2\) przyjmuje wartości ujemne a kiedy większe bądź równe zero.
\(x+1 \geqslant 0 \:\:\:\:\:\:\: x-2 \geqslant 0\)
\(x \geqslant -1 \:\:\:\:\:\:\: x \geqslant 2\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania naniesiemy je na oś:

Zgodnie z wyznaczonymi przedziałami: 1) \( (-\infty;-1)\) ; 2) \( \left \langle -1;2 \right )\) ; 3) \( \left \langle 2;+\infty \right )\), będziemy rozwiązywać nierówność w trzech etapach.
1) dla \( x \: \epsilon \: (-\infty;-1)\)
W tym przedziale wyrażenia \(x+1\) oraz \(x-2\) przyjmują wartości ujemne, dlatego przy opuszczaniu wartości bezwzględnej zmienimy znak obu wyrażeń:
\(|x+1|+|x-2|<4\)
\(|x+1|+|x-2|<4\)
\(-(x+1)-(x-2)<4\)
\(-x-1-x+2<4\)
\(-2x<4+1-2\)
\(-2x<3\)
\(x>-1\frac{1}{2}\)
Rozwiązując nierówność otrzymaliśmy \(x \: \epsilon \: (-1\dfrac{1}{2};+\infty)\) jednak całość rozpatrujemy tylko w przedziale \((-\infty;-1)\). Co oznacza, że musimy wybrać część wspólną tych zbiorów, a więc:
\((-1\dfrac{1}{2};+\infty) \cap (-\infty;-1) = (-1\dfrac{1}{2};-1)\)
Rozwiązaniem nierówności w tym przedziale jest więc \(x \: \epsilon \: (-1\dfrac{1}{2};-1)\).
2) dla \(x\: \epsilon \: \left \langle -1;2 \right )\)
W tym przedziale wyrażenie \(x+1\) przyjmuje wartości dodatnie, dlatego przy opuszczaniu wartości bezwzględnej nie zmienimy znaku tego wyrażenia. Wyrażenie \(x-2\) w tym przedziale przyjmuje wartości ujemne, przy opuszczaniu wartości bezwzględnej zmieniamy znak wyrażenia.
\(|x+1|+|x-2|<4\)
\(x+1-(x-2)<4\)
\(x+1-x+2<4\)
\(3<4\)
Otrzymaliśmy wyrażenie zawsze prawdziwe, oznacza to, że w tym przedziale wszystkie \(x\) są rozwiązaniem. Podsumowując, rozwiązaniem równania w tym przedziale jest \(x\: \epsilon \: \left \langle -1;2 \right )\).
3) dla \(x \: \epsilon \: \left \langle 2;+\infty \right )\)
w tym przedziale wyrażenia przyjmują wartości dodatnie. Oznacza to, że opuszczając wartość bezwzględna nie zmieniamy ich znaku:
\(|x+1|+|x-2|<4\)
\(x+1+x-2<4\)
\(2x<4-1+2\)
\(2x<5\)
\(x<2\dfrac{1}{2}\)
Otrzymaliśmy \(x\: \epsilon (-\infty;2\dfrac{1}{2})\) jednak rozpatrując to w przedziale \(\left \langle 2;+\infty \right )\), rozwiązaniem nierówności w danym przedziale jest: \( \left \langle 2; 2\dfrac{1}{2} \right )\).
Odpowiedź: Rozwiązaniem nierówności jest \(x\: \left( -1\dfrac{1}{2}; 2\dfrac{1}{2} \right )\)
c)
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
Na początku sprawdzamy, kiedy wyrażenia \(x+1\), \(x-2\) oraz \(x-3\) przyjmują wartości ujemne a kiedy większe bądź równe zero.
\(x+1 \geqslant 0 \:\:\:\:\:\:\: x-2 \geqslant 0 \:\:\:\:\:\:\: x-3 \geqslant 0\)
\(x \geqslant -1 \:\:\:\:\:\:\: x \geqslant 2 \:\:\:\:\:\:\: x \geqslant 3\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania naniesiemy je na oś:
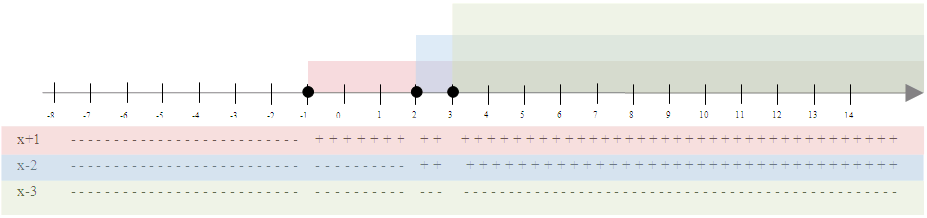
Po naniesieniu na oś mamy wyznaczone cztery przedziały: 1) \((-\infty;-1)\); 2) \(\left \langle -1;2 \right )\), 3) \(\left \langle 2;3 \right )\), 4) \(\left \langle 3;+\infty \right )\).
1) dla \(x \: \epsilon \: (-\infty;-1)\)
Wyrażenia \(x+1\), \(x-2\) oraz \(x-3\) przyjmują wartości ujemne, oznacza to, że przy opuszczaniu wartości bezwzględnej zmienimy znak wyrażeń:
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(-(x+1)-(x-2)-(x-3)\leqslant 11\)
\(-x-1-x+2-x+3\leqslant 11\)
\(-3x\leqslant 7\)
\(x\geqslant -2\dfrac{1}{3}\)
Rozwiązując nierówność otrzymaliśmy \((-2\dfrac{1}{3};+\infty)\) trzeba jednak rozpatrywać go w przedziale \((-\infty;-1)\). Rozwiązaniem nierówności w danym przedziale jest \( x \: (-2\dfrac{1}{3};-1)\).
2) dla \(x \: \epsilon \: \left \langle -1;2 \right )\)
Dla tego przedziału tylko \(x+1\) przyjmuje wartości dodatnie (więc przy opuszczaniu wartości bezwzględnej nie zmieniamy znaku), w pozostałych wyrażeniach zmieniamy znak.
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1-(x-2)-(x-3)\leqslant 11\)
\(x+1-x+2-x+3\leqslant 11\)
\(-x\leqslant 11-6\)
\(-x\leqslant 5\)
\(x\geqslant -5\)
Otrzymaliśmy rozwiązanie \(\left \langle -5;+\infty \right )\) jednak w danym przedziale będzie rozwiązaniem nierówności będzie \(x\: \epsilon \left \langle -1;2 \right )\).
3) dla \(x \: \epsilon \left \langle 2;3 \right )\)
W danym przedziale przy opuszczaniu wartości bezwzględnych nie zmieniamy znaku w wyrażeniach \(x+1\) oraz \(x-2\), natomiast w wyrażeniu \(x-3\) następuje zmiana znaku.
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1+x-2-(x-3)\leqslant 11\)
\(x+1+x-2-x+3\leqslant 11\)
\(x\leqslant 9\)
Mamy \(\left ( -\infty;9 \right \rangle\) rozpatrując jednak w przedziale \(\left \langle 2;3 \right )\) otrzymujemy rozwiązanie \(x \: \epsilon \left \langle 2;3 \right )\).
4) dla \(x \: \epsilon \left \langle 3;+\infty \right )\)
Wszystkie wyrażenia w tym przedziale przyjmują wartości dodatnie, co oznacza, że opuszczając wartości bezwzględne nie zmieniamy ich znaku:
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1+x-2+x-3\leqslant 11\)
\(3x\leqslant 11+4\)
\(3x\leqslant 15\)
\(x\leqslant 5\)
Po uwzględnieniu rozwiązania i przedziału otrzymujemy rozwiązanie \(x \: \epsilon \left \langle 3;5 \right )\).
Rozwiązaniem nierówności jest suma wszystkich rozwiązań, czyli:
\((-2\dfrac{1}{3};-1) \cup \left \langle -1;2 \right ) \cup \left \langle 2;3 \right ) \cup \left \langle 2;5 \right )=(-2\dfrac{1}{3};5)\)
Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: (-2\dfrac{1}{3};5)\).
Zadanie 1
Zadanie 2
Zadanie 3
a) \(|x-5|+|x+6|>11\) b) \(|x+1|+|x-2|<4\)
c) \(|x+1|+|2-x|+|x-3|\leqslant 11\)
Aby rozwiązać nierówność tego typu najpierw podzielimy nierówność na kilka przypadków, zależnych od przyjmowanego znaku wyrażenia pod wartością bezwzględną.
Rozwiązanie
a)
\(|x-5|+|x+6|>11\)
Na początku postępujemy jak przy równaniu, czyli sprawdzamy, kiedy \(x-5\) oraz \(x+6\) przyjmuje wartości ujemne a kiedy większe bądź równe zero.
\(x-5 \geqslant 0 \:\:\:\:\:\:\: x+6 \geqslant 0\)
\(x \geqslant 5 \:\:\:\:\:\:\: x \geqslant -6\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania lepiej najpierw nanieść je na oś:

Rozwiązywanie nierówności podzielimy na trzy części zgodnie z przedziałami wyznaczonymi na osi.
1) dla \( x \: \epsilon \: (-\infty;-6)\)
Wyrażenia \(x-5\) oraz \(x+6\) w danym przedziale przyjmują wartości ujemne, dlatego przy opuszczaniu wartości bezwzględnych zmienimy ich znak.
\(|x-5|+|x+6|>11\)
\(-(x-5)-(x+6)>11\)
\(-x+5-x-6>11\)
\(-2x>11-5+6\)
\(-2x>12\)
\(x<-6\)
Rozwiązując nierówność otrzymaliśmy \(x \: \epsilon \: (-\infty,-6)\) należy to do przedziału więc \(x \: \epsilon \: (-\infty,-6)\) jest rozwiązaniem nierówności.
2) dla \( x \: \epsilon \: \left \langle -6;5 \right )\)
W podanym przedziale wyrażenie \(x-5\) przyjmuje wartości ujemne, dlatego opuszczając wartość bezwzględną zmienimy znak wyrażenia. Wyrażenie \(x+6\) w podanym przedziale przyjmuje wartości dodatnie, dlatego opuszczając wartość bezwzględna nie zmieniamy znaku wyrażenia.
\(|x-5|+|x+6|>11\)
\(-(x-5)+x+6>11\)
\(-x+5+x+6>11\)
\(11>11\)
Rozwiązując nierówność otrzymaliśmy wyrażenie sprzeczne, ponieważ 11 nie jest większe od 11. Oznacza to, że w przedziale \(\left \langle -6;5 \right )\) nie ma \(x\)-ów będących rozwiązaniem nierówności.
3) dla \( x \: \epsilon \: \left \langle 5;+\infty \right )\)
W podanym przedziale wyrażenia \(x-5\) oraz \(x+6\) przyjmując wartości dodatnie, oznacza to, że opuszczając wartość bezwzględną nie zmieniamy znaków wyrażeń.
\(|x-5|+|x+6|>11\)
\(x-5+x+6>11\)
\(2x>11+5-6\)
\(2x>10\)
\(x>5\)
Rozwiązując nierówność otrzymaliśmy \(x \epsilon (5;+\infty)\), należy on do naszego przedziału. Oznacza to, że rozwiązaniem nierówności jest \(x \epsilon (5;+\infty)\).
Odpowiedź: Rozwiązaniem nierówności jest \( x \: \epsilon \: (-\infty,-6) \: \cup \: (5;+\infty)\).
b)
\(|x+1|+|x-2|<4\)
Na początku sprawdzamy, kiedy \(x+1\) oraz \(x-2\) przyjmuje wartości ujemne a kiedy większe bądź równe zero.
\(x+1 \geqslant 0 \:\:\:\:\:\:\: x-2 \geqslant 0\)
\(x \geqslant -1 \:\:\:\:\:\:\: x \geqslant 2\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania naniesiemy je na oś:

Zgodnie z wyznaczonymi przedziałami: 1) \( (-\infty;-1)\) ; 2) \( \left \langle -1;2 \right )\) ; 3) \( \left \langle 2;+\infty \right )\), będziemy rozwiązywać nierówność w trzech etapach.
1) dla \( x \: \epsilon \: (-\infty;-1)\)
W tym przedziale wyrażenia \(x+1\) oraz \(x-2\) przyjmują wartości ujemne, dlatego przy opuszczaniu wartości bezwzględnej zmienimy znak obu wyrażeń:
\(|x+1|+|x-2|<4\)
\(|x+1|+|x-2|<4\)
\(-(x+1)-(x-2)<4\)
\(-x-1-x+2<4\)
\(-2x<4+1-2\)
\(-2x<3\)
\(x>-1\frac{1}{2}\)
Rozwiązując nierówność otrzymaliśmy \(x \: \epsilon \: (-1\dfrac{1}{2};+\infty)\) jednak całość rozpatrujemy tylko w przedziale \((-\infty;-1)\). Co oznacza, że musimy wybrać część wspólną tych zbiorów, a więc:
\((-1\dfrac{1}{2};+\infty) \cap (-\infty;-1) = (-1\dfrac{1}{2};-1)\)
Rozwiązaniem nierówności w tym przedziale jest więc \(x \: \epsilon \: (-1\dfrac{1}{2};-1)\).
2) dla \(x\: \epsilon \: \left \langle -1;2 \right )\)
W tym przedziale wyrażenie \(x+1\) przyjmuje wartości dodatnie, dlatego przy opuszczaniu wartości bezwzględnej nie zmienimy znaku tego wyrażenia. Wyrażenie \(x-2\) w tym przedziale przyjmuje wartości ujemne, przy opuszczaniu wartości bezwzględnej zmieniamy znak wyrażenia.
\(|x+1|+|x-2|<4\)
\(x+1-(x-2)<4\)
\(x+1-x+2<4\)
\(3<4\)
Otrzymaliśmy wyrażenie zawsze prawdziwe, oznacza to, że w tym przedziale wszystkie \(x\) są rozwiązaniem. Podsumowując, rozwiązaniem równania w tym przedziale jest \(x\: \epsilon \: \left \langle -1;2 \right )\).
3) dla \(x \: \epsilon \: \left \langle 2;+\infty \right )\)
w tym przedziale wyrażenia przyjmują wartości dodatnie. Oznacza to, że opuszczając wartość bezwzględna nie zmieniamy ich znaku:
\(|x+1|+|x-2|<4\)
\(x+1+x-2<4\)
\(2x<4-1+2\)
\(2x<5\)
\(x<2\dfrac{1}{2}\)
Otrzymaliśmy \(x\: \epsilon (-\infty;2\dfrac{1}{2})\) jednak rozpatrując to w przedziale \(\left \langle 2;+\infty \right )\), rozwiązaniem nierówności w danym przedziale jest: \( \left \langle 2; 2\dfrac{1}{2} \right )\).
Odpowiedź: Rozwiązaniem nierówności jest \(x\: \left( -1\dfrac{1}{2}; 2\dfrac{1}{2} \right )\)
c)
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
Na początku sprawdzamy, kiedy wyrażenia \(x+1\), \(x-2\) oraz \(x-3\) przyjmują wartości ujemne a kiedy większe bądź równe zero.
\(x+1 \geqslant 0 \:\:\:\:\:\:\: x-2 \geqslant 0 \:\:\:\:\:\:\: x-3 \geqslant 0\)
\(x \geqslant -1 \:\:\:\:\:\:\: x \geqslant 2 \:\:\:\:\:\:\: x \geqslant 3\)
Te wyniki wskazują przedziały, w jakich będziemy rozwiązywali naszą nierówność, dla łatwiejszego zobrazowania naniesiemy je na oś:

Po naniesieniu na oś mamy wyznaczone cztery przedziały: 1) \((-\infty;-1)\); 2) \(\left \langle -1;2 \right )\), 3) \(\left \langle 2;3 \right )\), 4) \(\left \langle 3;+\infty \right )\).
1) dla \(x \: \epsilon \: (-\infty;-1)\)
Wyrażenia \(x+1\), \(x-2\) oraz \(x-3\) przyjmują wartości ujemne, oznacza to, że przy opuszczaniu wartości bezwzględnej zmienimy znak wyrażeń:
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(-(x+1)-(x-2)-(x-3)\leqslant 11\)
\(-x-1-x+2-x+3\leqslant 11\)
\(-3x\leqslant 7\)
\(x\geqslant -2\dfrac{1}{3}\)
Rozwiązując nierówność otrzymaliśmy \((-2\dfrac{1}{3};+\infty)\) trzeba jednak rozpatrywać go w przedziale \((-\infty;-1)\). Rozwiązaniem nierówności w danym przedziale jest \( x \: (-2\dfrac{1}{3};-1)\).
2) dla \(x \: \epsilon \: \left \langle -1;2 \right )\)
Dla tego przedziału tylko \(x+1\) przyjmuje wartości dodatnie (więc przy opuszczaniu wartości bezwzględnej nie zmieniamy znaku), w pozostałych wyrażeniach zmieniamy znak.
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1-(x-2)-(x-3)\leqslant 11\)
\(x+1-x+2-x+3\leqslant 11\)
\(-x\leqslant 11-6\)
\(-x\leqslant 5\)
\(x\geqslant -5\)
Otrzymaliśmy rozwiązanie \(\left \langle -5;+\infty \right )\) jednak w danym przedziale będzie rozwiązaniem nierówności będzie \(x\: \epsilon \left \langle -1;2 \right )\).
3) dla \(x \: \epsilon \left \langle 2;3 \right )\)
W danym przedziale przy opuszczaniu wartości bezwzględnych nie zmieniamy znaku w wyrażeniach \(x+1\) oraz \(x-2\), natomiast w wyrażeniu \(x-3\) następuje zmiana znaku.
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1+x-2-(x-3)\leqslant 11\)
\(x+1+x-2-x+3\leqslant 11\)
\(x\leqslant 9\)
Mamy \(\left ( -\infty;9 \right \rangle\) rozpatrując jednak w przedziale \(\left \langle 2;3 \right )\) otrzymujemy rozwiązanie \(x \: \epsilon \left \langle 2;3 \right )\).
4) dla \(x \: \epsilon \left \langle 3;+\infty \right )\)
Wszystkie wyrażenia w tym przedziale przyjmują wartości dodatnie, co oznacza, że opuszczając wartości bezwzględne nie zmieniamy ich znaku:
\(|x+1|+|x-2|+|x-3|\leqslant 11\)
\(x+1+x-2+x-3\leqslant 11\)
\(3x\leqslant 11+4\)
\(3x\leqslant 15\)
\(x\leqslant 5\)
Po uwzględnieniu rozwiązania i przedziału otrzymujemy rozwiązanie \(x \: \epsilon \left \langle 3;5 \right )\).
Rozwiązaniem nierówności jest suma wszystkich rozwiązań, czyli:
\((-2\dfrac{1}{3};-1) \cup \left \langle -1;2 \right ) \cup \left \langle 2;3 \right ) \cup \left \langle 2;5 \right )=(-2\dfrac{1}{3};5)\)
Odpowiedź: Rozwiązaniem nierówności jest \(x \: \epsilon \: (-2\dfrac{1}{3};5)\).
Zadanie 1
Zadanie 2
Zadanie 3
Jak obliczyć nierówności z wartością bezwzględną – zadanie 4 - wyniki