Wykres każdej funkcji kwadratowej nazywany jest parabolą. Każda parabola składa się z dwóch ramion. Jeżeli funkcja w postaci \(f(x)=ax^2+bx+c\) posiada współczynnik \(a>0\) większy od zera, to ramiona paraboli skierowane są do góry, np.:
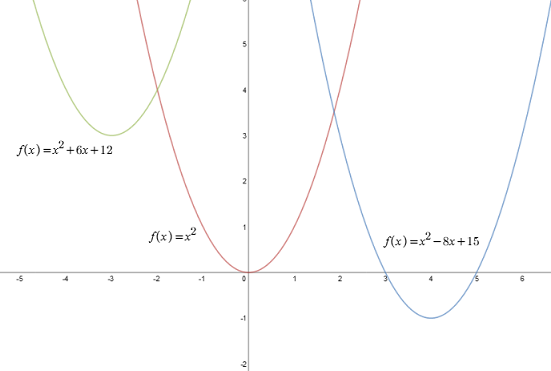
Jeżeli funkcja posiada współczynnik \(a<0\) mniejszy od zera, to ramiona paraboli skierowane są ku dołowi, np.:
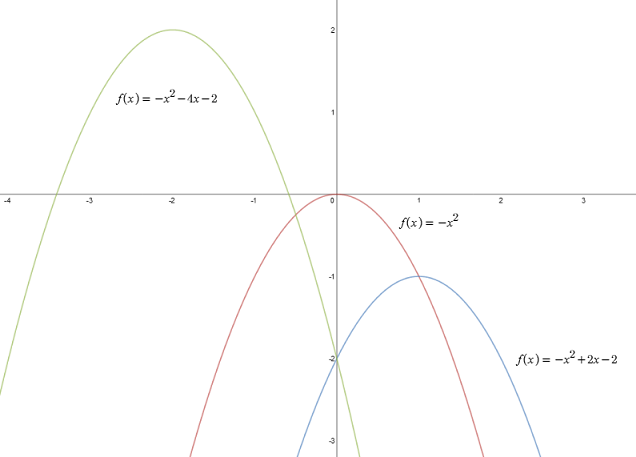
Każda parabola posiada swój wierzchołek, jest to punkt najdalej wysunięty. Wierzchołek jest również miejscem, w którym funkcja kwadratowa zmienia się z rosnącej na malejącą lub z malejącej na rosnącą.
Współrzędne wierzchołka paraboli to \(W=(p;q)\), dla funkcji kwadratowej w postaci ogólnej \(f(x)=ax^2+bx+c\) to:
\(p=-\frac{b}{2a}\)
\(q=-\frac{\Delta}{4a}\) gdzie \(\Delta=b^2-4ac\)
Postać kanoniczna funkcji kwadratowej to:
\(f(x)=a(x-p)^2+q\)
W łatwy sposób możemy z niej odczytać współrzędne wierzchołka paraboli.
Przykład
\(f(x)=(x-{\color{Green}{2}})^2+{\color{Green} {5}}\)
Wierzchołek paraboli znajduje się w punkcie \((2;5)\).
Własności funkcji kwadratowej \(f(x)=ax^2+bx+c\):
1) Dziedzina – wszystkie liczby rzeczywiste - \(D_f=R\)
2) Zbiór wartości
– dla \(a>0\) - \(ZW=\left \langle -\frac{\Delta}{4a};+\infty \right )\)
– dla \(a<0\) - \(ZW=\left ( -\infty;-\frac{\Delta}{4a} \right \rangle\)
3) Miejsca zerowe z zależności od Δ
- dla \(\Delta>0\) – dwa miejsca zerowe \(x_1=\frac{-b + \sqrt{ \Delta }}{ 2a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: x_2 = \frac{-b - \sqrt{ \Delta }}{2a}\),
- dla \(\Delta=0\) – jedno miejsce zerowe \(x_1=x_2=-\frac{b}{2a}\),
- dla \(\Delta<0\) – brak miejsc zerowych,
4) punkt przecięcia z osią OY to \((0;c)\)
5) monotoniczność w zależności od parametru \(a\):
- dla \(a>0\) - funkcja rośnie dla \(x \: \epsilon \: \left ( -\frac{b}{2a};+\infty \right )\), maleje dla \(x \: \epsilon \: \left ( -\infty;-\frac{b}{2a} \right )\)
- dla \(a<0\) - funkcja maleje dla \(x \: \epsilon \: \left ( -\frac{b}{2a};+\infty \right )\), rośnie dla \(x \: \epsilon \: \left ( -\infty;-\frac{b}{2a} \right )\)
6) Wierzchołek paraboli znajduje się w punkcie \(W=(p;q)\) gdzie:
\(p=-\frac{b}{2a}\)
\(q=-\frac{\Delta}{4a}\) gdzie \(\Delta=b^2-4ac\)
7) Funkcja nie jest różnowartościowa
Są to uniwersalne dane dla każdej funkcji kwadratowej, określenie wartości dodatnich i ujemnych, parzystości, etc., rozpatruje się na konkretnych przypadkach, ponieważ opisanie ich w postaci uniwersalnej byłoby dość skomplikowane.
Przykładowe zadania
Zad. 1) Czy podana funkcja kwadratowa ma ramiona skierowane w górę czy w dół, podaj miejsce przecięcia z osią OY
a) \(f(x)=x^2-8x+12\)
b) \(f(x)=-x^2+5x-4\)
c) \(f(x)=x^2-2x\)
d) \(f(x)=x^2\)
e) \(f(x)=x^2+6x+10\) Zobacz rozwiązanie
Zad. 2) Podaj współrzędne wierzchołka paraboli:
a) \( f(x)=x^2+3x-2\)
b) \( f(x)=x^2+4x+4\)
c) \( f(x)=2x^2-12x-6\)
d) \( f(x)=-x^2+x-8\)
e) \(f(x)=x^2+8x-15\) Zobacz rozwiązanie
Zad. 3) Zbadaj monotoniczność funkcji kwadratowej.
a) \(f(x)=2x^2+3x+7\)
b) \(f(x)=5x^2-2=\)
c) \(f(x)=x^2-3x-7\)
d) \(f(x)=3x-2x^2-8\)
e) \(f(x)=90+x^2-3x\) Zobacz rozwiązanie
Zad. 4) Oblicz zbiór wartości funkcji kwadratowej:
a) \(f(x)=x^2+3x-2\)
b) \(f(x)=x^2+4x+4\)
c) \(f(x)=2x^2-12x-6\)
d) \(f(x)=-x^2+x-8\)
e) \( f(x)=x^2+8x-15\) Zobacz rozwiązanie
Wykres funkcji kwadratowej Wasze opinie